实例介绍
【实例简介】快速傅里叶变换(Fast Fourier Transform)是离散傅里叶变换的一种快速算法,简称FFT,通过FFT可以将一个信号从时域变换到频域。
模拟信号经过A/D转换变为数字信号的过程称为采样。为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的2倍,这称之为采样定理。
假设采样频率为fs,采样点数为N,那么FFT结果就是一个N点的复数,每一个点就对应着一个频率点,某一点n(n从1开始)表示的频率为:fn=(n-1)*fs/N。
举例说明:用1kHz的采样频率采样128点,则FFT结果的128个数据即对应的频率点分别是0,1k/128,2k/128,3k/128,…,127k/128 Hz。
这个频率点的幅值为:该点复数的模值除以N/2(n=1时是直流分量,其幅值是该点的模值除以N)。
【实例截图】
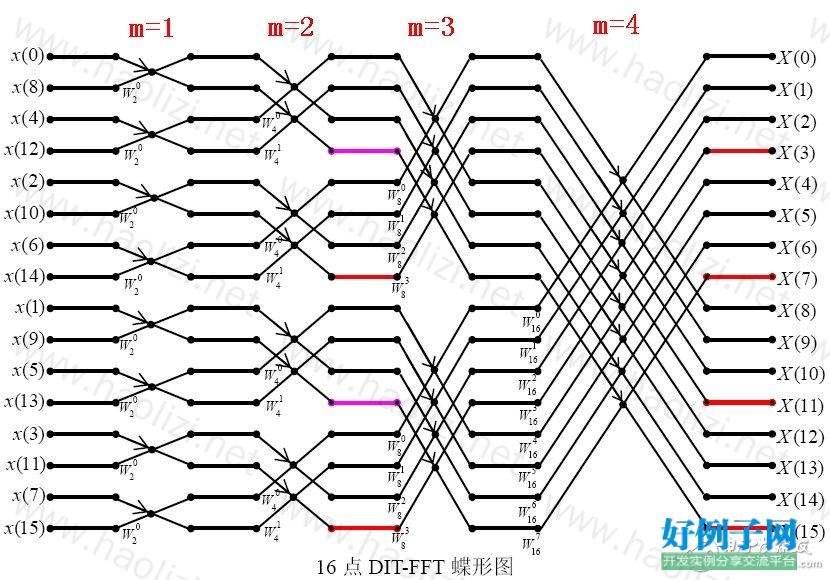
【核心代码】/***【快速傅里叶变换】***/
void FFT(void)
{
unsigned int i,j,k,l;
complex top,bottom,xW;
Reverse(); //码位倒序
for(i=0;i
{ //一级蝶形运算
l=1<
for(j=0;j
{ //一组蝶形运算
for(k=0;k
{ //一个蝶形运算
xW=mul(x[j k l],WN[N/(2*l)*k]); //碟间距为l
top=add(x[j k],xW); //每组的第k个蝶形
bottom=sub(x[j k],xW);
x[j k]=top;
x[j k l]=bottom;
}
}
}
}
模拟信号经过A/D转换变为数字信号的过程称为采样。为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的2倍,这称之为采样定理。
假设采样频率为fs,采样点数为N,那么FFT结果就是一个N点的复数,每一个点就对应着一个频率点,某一点n(n从1开始)表示的频率为:fn=(n-1)*fs/N。
举例说明:用1kHz的采样频率采样128点,则FFT结果的128个数据即对应的频率点分别是0,1k/128,2k/128,3k/128,…,127k/128 Hz。
这个频率点的幅值为:该点复数的模值除以N/2(n=1时是直流分量,其幅值是该点的模值除以N)。
【实例截图】

【核心代码】/***【快速傅里叶变换】***/
void FFT(void)
{
unsigned int i,j,k,l;
complex top,bottom,xW;
Reverse(); //码位倒序
for(i=0;i
{ //一级蝶形运算
l=1<
for(j=0;j
{ //一组蝶形运算
for(k=0;k
{ //一个蝶形运算
xW=mul(x[j k l],WN[N/(2*l)*k]); //碟间距为l
top=add(x[j k],xW); //每组的第k个蝶形
bottom=sub(x[j k],xW);
x[j k]=top;
x[j k l]=bottom;
}
}
}
}
好例子网口号:伸出你的我的手 — 分享!
小贴士
感谢您为本站写下的评论,您的评论对其它用户来说具有重要的参考价值,所以请认真填写。
- 类似“顶”、“沙发”之类没有营养的文字,对勤劳贡献的楼主来说是令人沮丧的反馈信息。
- 相信您也不想看到一排文字/表情墙,所以请不要反馈意义不大的重复字符,也请尽量不要纯表情的回复。
- 提问之前请再仔细看一遍楼主的说明,或许是您遗漏了。
- 请勿到处挖坑绊人、招贴广告。既占空间让人厌烦,又没人会搭理,于人于己都无利。
关于好例子网
本站旨在为广大IT学习爱好者提供一个非营利性互相学习交流分享平台。本站所有资源都可以被免费获取学习研究。本站资源来自网友分享,对搜索内容的合法性不具有预见性、识别性、控制性,仅供学习研究,请务必在下载后24小时内给予删除,不得用于其他任何用途,否则后果自负。基于互联网的特殊性,平台无法对用户传输的作品、信息、内容的权属或合法性、安全性、合规性、真实性、科学性、完整权、有效性等进行实质审查;无论平台是否已进行审查,用户均应自行承担因其传输的作品、信息、内容而可能或已经产生的侵权或权属纠纷等法律责任。本站所有资源不代表本站的观点或立场,基于网友分享,根据中国法律《信息网络传播权保护条例》第二十二与二十三条之规定,若资源存在侵权或相关问题请联系本站客服人员,点此联系我们。关于更多版权及免责申明参见 版权及免责申明



网友评论
我要评论